More actions
किसी वस्तु के वेग मे परिवर्तन की दर को त्वरण (Acceleration) कहते हैं। इसका मात्रक मीटर प्रति सेकेण्ड2 होता है तथा यह एक सदिश राशि हैं।
- <math>\vec a(t) = \frac{\mathrm{d}\vec v(t)}{\mathrm{d}t} \equiv \dot{\vec v}(t)</math>
या,
- <math>\vec a(t) = \frac{\mathrm{d}^2\vec r(t)}{\mathrm{d} t^2} \equiv \ddot{\vec r}(t)</math>
उदाहरण: माना समय t=० पर कोई कण १० मीटर/सेकेण्ड के वेग से उत्तर दिशा में गति कर रहा है। १० सेकेण्ड बाद उसका वेग बढ़कर ३० मीटर/सेकेण्ड (उत्तर दिशा में) हो जाता है। यह मानते हुए कि इस समयान्तराल में त्वरण का मान नियत है, त्वरण का मान
- = (३० m/s - १० m/s) / १० सेकेण्ड = २ मीटर प्रति सेकेण्ड2 होगा।
- किसी वस्तु विशेष द्वारा बदला गया वेग ही त्वरण Acceleration कहलाता है।
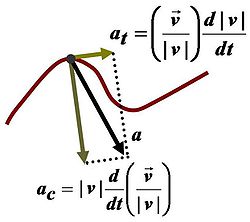
स्पर्शरेखीय तथा अभिकेंद्रीय त्वरण
किसी वक्र पथ पर गति करते हुए कण का वेग समय के फलन के रूप में निम्नलिखित प्रकार से लिखा जा सकता है-
- <math>\mathbf{v} (t) =v(t) \frac {\mathbf{v}(t)}{v(t)} = v(t) \mathbf{u}_\mathrm{t}(t), </math>
जहाँ v(t) पथ की दिशा में वेग है, तथा
- <math>\mathbf{u}_\mathrm{t} = \frac {\mathbf{v}(t)}{v(t)} \, </math>
गति की दिशा में गतिपथ के स्पर्शरेखीय इकाई सदिश है। ध्यान दें कि यहाँ v(t) तथा ut दोनों समय के साथ परिवर्तन्शील हैं, त्वरण की गणना निम्नलिखित प्रकार से की जायेगी:[२]
- <math>\begin{alignat}{3}
\mathbf{a} & = \frac{\mathrm{d} \mathbf{v}}{\mathrm{d}t} \\
& = \frac{\mathrm{d}v }{\mathrm{d}t} \mathbf{u}_\mathrm{t} +v(t)\frac{d \mathbf{u}_\mathrm{t}}{dt} \\
& = \frac{\mathrm{d}v }{\mathrm{d}t} \mathbf{u}_\mathrm{t}+ \frac{v^2}{r}\mathbf{u}_\mathrm{n}\, \\
\end{alignat}</math>
जहाँ un इकाई नॉर्मल सदिश (अन्दर की तरफ) है तथा r उस क्षण पर वक्रता त्रिज्या है। त्वरन के इन दो घटकों को क्रमशः स्पर्शरेखीय त्वरण (tangential acceleration) तथा नॉर्मल त्वरन या त्रिज्य त्वरण या अभिकेन्द्रीय त्वरण (centripetal acceleration) कहते हैं।
कुछ विशिष्ट स्थितियाँ
- रैखिक गति
- वृत्तीय गति
- सरल आवर्त गति (सिम्पल हार्मोनिक मोशन)
- परवलयिक गति - त्वरण का परिमाण और दिशा अचर हो, वेग का परिमाण और दिशा परिवर्ती हो; जैसे प्रक्षेप्य गति)
सन्दर्भ
इन्हें भी देखें
- त्वरणमापी
- भूकम्पमापी
- गुरुत्वजनित त्वरण
- न्यूटन का गति का दूसरा नियम
- कण त्वरक
- उपरोधी वाल्व (थ्रॉटिल वाल्व) या मोटरगाड़ियों का त्वरक (एक्सलरेटर)
बाहरी कड़ियाँ
- Acceleration Calculator Simple acceleration unit converter
- Measurespeed.com - Acceleration Calculator Based on starting & ending speed and time elapsed.